
移動平均線は市場のトレンドを分析するための重要なツールであり、いくつかの異なる種類があります。以下に主要な移動平均線とその計算式を説明します。
単純移動平均 (SMA: Simple Moving Average)
単純移動平均(SMA: Simple Moving Average)は、時系列データの平均を求める最も基本的な手法の一つです。これは各データポイントに同じ重みを与え、一定期間内の平均値を計算します。
計算方法
単純移動平均は以下のように計算されます。

ここで、価格1,価格2,…,価格n価格1,価格2,…,価格nは時系列データ(例えば株価や気温など)の値であり、nnは平均を取る期間(日数、時間数、サンプル数など)です。
例
たとえば、5日間の単純移動平均を計算する場合は以下のようになります。

単純移動平均は計算が容易であり、理解もしやすいため多くの分野で広く使用されています。しかし、すべてのデータに等しく重みを付けるため、最新のデータの動きにはあまり敏感ではないという特性があります。この点は、より高度な移動平均手法(例:EMA、WMAなど)が試みて補完する部分です。
指数移動平均 (EMA: Exponential Moving Average)
指数移動平均(EMA: Exponential Moving Average)は、時系列データの平均を求める方法の一つで、最近のデータに高い重みを置く計算手法です。EMAは金融市場でのテクニカル分析や、シグナル処理、統計学などさまざまな場面で使用されます。
計算方法
指数移動平均は以下のように計算されます。

または

ここで、α(アルファ)は平滑化定数と呼ばれ、通常は0<α≤10<α≤1の範囲で設定されます。この平滑化定数が大きいほど、最新の価格に対する反応が敏感になります。一般には、αは以下のように計算されることが多いです。
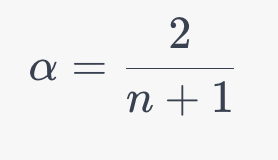
ここでnnは移動平均の期間(日数や時間数など)です。
例
例えば、5日間のEMAを計算する場合、ααは次のようになります。
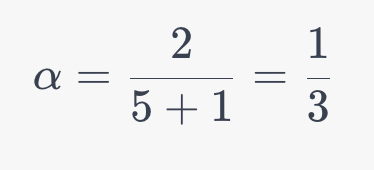
このαと価格データを用いて、上記のEMAの公式に従って計算を行います。
加重移動平均 (WMA: Weighted Moving Average)
加重移動平均(WMA: Weighted Moving Average)は、時系列データの平均を求める手法の一つで、最近のデータに高い重みを置くことが特徴です。シンプルな移動平均(SMA: Simple Moving Average)が各データポイントに等しい重みを置くのに対して、加重移動平均では各データポイントに異なる重みが割り当てられます。
計算方法
加重移動平均は以下のように計算されます。
WMA=w1×価格1+w2×価格2+…+wn×価格nw1+w2+…+wnWMA=w1+w2+…+wnw1×価格1+w2×価格2+…+wn×価格n
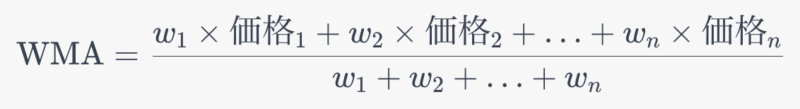
ここで、w1,w2,…,wnw1,w2,…,wnは各データポイントに割り当てられた重みであり、価格1,価格2,…,価格n価格1,価格2,…,価格nは時系列データ(例えば株価など)の値です。
一例
加重移動平均の一般的な形では、最新のデータポイントに最も高い重みが割り当てられ、その前のデータポイントには少しずつ小さな重みが割り当てられます。例えば、3日間の加重移動平均を考えると:
WMA=3×価格3+2×価格2+1×価格13+2+1=3×価格3+2×価格2+1×価格16WMA=3+2+13×価格3+2×価格2+1×価格1=63×価格3+2×価格2+1×価格1

このような加重移動平均は、時系列データの「ノイズ」を平滑化しつつ、最新の動きに敏感に反応するための手法として多くの場面で用いられています。特に金融市場でのテクニカル分析などによく使われます。
4. 三角移動平均 (TMA: Triangular Moving Average)
三角移動平均(TMA: Triangular Moving Average)は、シンプルな移動平均(SMA: Simple Moving Average)を二度適用することで計算される平均化手法です。これにより、データの平滑化が一層強化され、中央の値により重みが置かれます。
計算方法
三角移動平均は次の手順で計算されます。
第一段階のSMA計算: まず、指定された期間 nn にわたるシンプルな移動平均(SMA)を計算します。SMA1=価格1+価格2+…+価格nnSMA1=n価格1+価格2+…+価格n

第二段階のSMA計算: 第一段階で計算されたSMAに対して、再度SMAを計算します。この第二段階のSMAが三角移動平均(TMA)です。TMA=SMA1,1+SMA1,2+…+SMA1,nnTMA=nSMA1,1+SMA1,2+…+SMA1,n
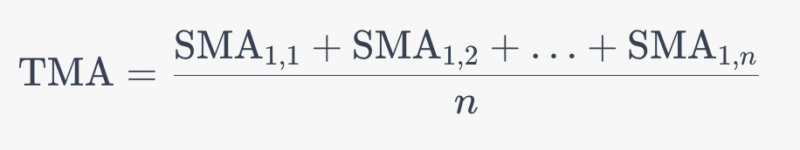
このようにして計算されたTMAは、データの中央に重みをより強く置く特性があります。
例
例として、5日の三角移動平均を計算する場合を考えましょう。
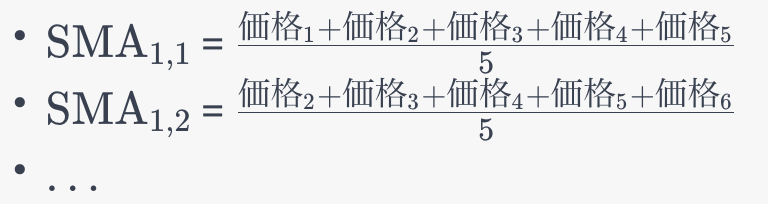
第一段階: 各5日ごとのSMAを計算します。
SMA1,1SMA1,1 = 価格1+価格2+価格3+価格4+価格555価格1+価格2+価格3+価格4+価格5
SMA1,2SMA1,2 = 価格2+価格3+価格4+価格5+価格655価格2+価格3+価格4+価格5+価格6
……
第二段階: 各5日ごとの第一段階のSMAのSMAを計算します。
TMA1TMA1 = SMA1,1+SMA1,2+…+SMA1,555SMA1,1+SMA1,2+…+SMA1,5
TMA2TMA2 = SMA1,2+SMA1,3+…+SMA1,655SMA1,2+SMA1,3+…+SMA1,6
……

これが三角移動平均(TMA)の基本的な計算方法です。この平均法は、市場のトレンドをより滑らかに捉えたい場合に使用されます。
変動移動平均 (VMA: Variable Moving Average)
変動移動平均は、市場のボラティリティに応じて調整される動的な期間を使用します。
変動移動平均(Variable Moving Average, VMA)は一般に特定のアルゴリズムや戦略に依存していますので、一様な計算式が存在するわけではありません。しかし、一つの典型的な方法として、以下のような計算式がよく使用されます。

ここで、α(アルファ)は変動する平滑化係数です。この値は通常0と1の間であり、この値によってどれだけ過去のデータに依存するのかを調整します。変動すると言われるのは、このααが一定ではなく、何らかの条件や別のインジケータに基づいて動的に調整される点です。
たとえば、市場が非常に変動性が高い場合にはααを小さくして過去のデータにより依存するようにし、逆に市場が安定している場合にはααを大きくしてより最近のデータに依存するようにする、といった調整が可能です。
このαの値をどのように設定するか、またはどのような条件で変更するかは、具体的な戦略や目的によって大きく異なります。それによって、VMAがどれだけ反応性が高く、または平滑化されるかが決まります。
ワイルダーの平滑化移動平均 (Wilder’s Smoothing)
ワイルダーの平滑化移動平均(Wilder’s Smoothing)は、J. Welles Wilderによって開発された特殊な形の指数移動平均(EMA)です。これは特に金融市場におけるテクニカル分析でよく使用されます。Wilder’s Smoothingは主にWilderが開発した他のテクニカル指標、たとえば相対力指数(RSI)や平均真の範囲(ATR)などと併用されることが多いです。
計算方法
ワイルダーの平滑化移動平均は以下のように計算されることが一般的です。

ここで、nnは平均を取る期間(日数、時間数など)です。
例
たとえば、14日間のWilder’s Smoothingを計算する場合:
- 初日のWilder’s Smoothingは、最初の14日間の価格の単純平均となります。

- 2日目以降は、前日のWilder’s Smoothingと今日の価格を用いて計算します。

このようにして、ワイルダーの平滑化移動平均は計算されます。この平均法は、特にWilderが開発したテクニカル指標と組み合わせて使用されることが多く、金融市場でのトレンドやボラティリティの分析に役立ちます。
まとめ
これらの移動平均線は、トレーダーが市場のトレンドを分析し、トレーディングの決定を下すのに役立つツールとして使用されます。

